【论文笔记】Data-Free Model Extraction(CVPR 2021)
(还不是很完善orz)
本文证明并解决了现有model extraction对数据集的依赖(依赖于替代数据集与实际训练集的相似性),并且在目标模型以black box形式被访问的条件下,提出了data-free的model extraction攻击,称为data-free model extraction (DFME)。DFME中采用了data-free knowledge transfer中的一些技术。
- ⭕利用GAN网络来训练攻击模型,其中一个generator负责生成训练数据,另一个student model来学习目标模型在这些数据上的行为(做到data free)
- ⭕使用$l_1$范式损失函数(防止梯度消失)
- 使用零阶优化(前向差分法)来逼近梯度(解决目标模型是个black box,无法获知其真实梯度的问题)
- ⭕从概率向量中还原目标模型的logits
1 相关工作
1.1 Data-Free Knowledge Distillation(无数据知识蒸馏)
可参考https://zhuanlan.zhihu.com/p/516930757、https://zhuanlan.zhihu.com/p/102038521(知识蒸馏)
知识蒸馏是一种模型压缩方法,是一种基于“teacher-student网络思想”的训练方法,目标是把一个训练好的模型(teacher,Net-T)的知识压缩给另外一个模型(student,Net-S),达到节省模型训练的开销的作用。其中,Net-T一般结构复杂、参数量大,而Net-S结构较为简单、参数量小。那么在用Net-T来训练Net-S的时候,就是让Net-S去学习Net-T的泛化能力,直接的办法是使用softmax层输出的类别的概率来作为“soft target”。
soft target相对应的是hard target。一般的标签都是hard target,就是说一个对象只有一个标签。而soft target则是在每个标签上都有一定的值。举例来说,一个写的像3的2,在”3”上具有一定的概率值。而写的像7的2,在”7”上有一定的概率值,那么他们就提供了更多的信息。
【参考】https://antkillerfarm.github.io/dl%20acceleration/2019/07/27/DL_acceleration_6.html
使用soft target来训练Net-S时,softmax函数就变成了如下的形式

(具体先不展开,看看之后需要用到哪些KD相关的知识再说)
1.2 Generative Models
本文中使用GAN类似的方法去训练student,用GAN去拟合最能说明当前student和teacher的决策曲面之间差异的数据分布(好复杂。。。)
1.3 Black-box Gradient Approximation
因为目标模型是个black box,无法获得其梯度,所以采用的是零阶优化的方式来做到梯度逼近(之后会再介绍)
2 How Hard is it to Find a Surrogate Dataset?
实验证明了现有model extraction都是基于替代数据集(surrogate dataset)非常接近与原始训练集的,若是替代集和原始训练集差别比较大,攻击的准确率就会低。
但是这样的surrogate dataset在现实中难以获得,于是作者提出了DFME
3 Data-Free Model Extraction
介绍了本文提出的攻击方法
DFME的目标是使extraction model对x的预测和目标模型对x的预测不同的概率最小。其中$D_V$是目标模型的训练集(攻击者不可知),所以可以用合成的数据集$D_S$
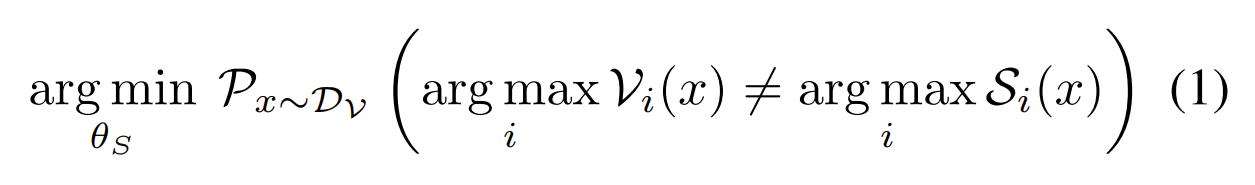
训练extraction model时,优化时使用的损失函数是$L$,则要满足
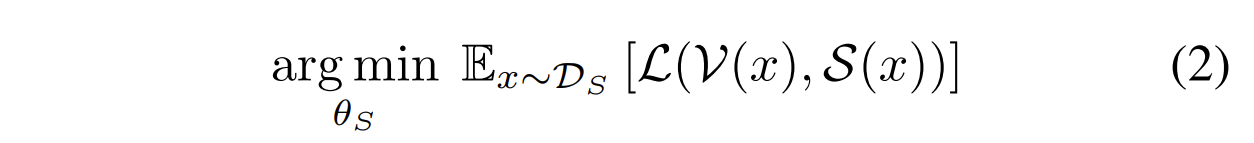
3.1 Overview
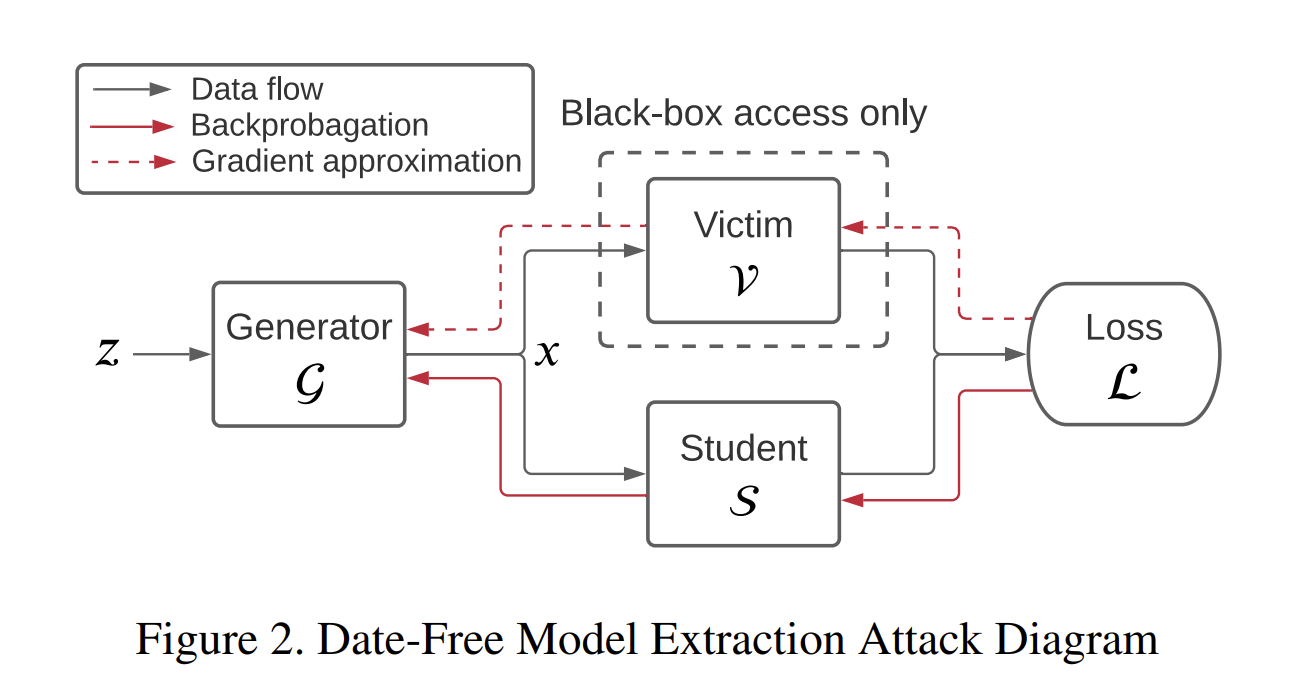
GFME的过程就是一个GAN网络,generator $G$生成输入$x$,目标网络$V$和Student网络$S$作为discriminator,$S$要去学习$V$对输入$x$的预测行为。其中$z$是一个随机的噪音,$G$通过给到的$z$来生成输入$x$。然后通过反向传播来优化。但是目标模型$V$是black-box,所以只能采取梯度逼近的方法。$G$和$S$一起组成了攻击模型。
关于Student model $S$的结构的选择
只需要知道目标模型所解决的问题的一般知识,选择适合的模型结构即可(根据知识蒸馏工作发现的结果)
关于损失函数的选择:
这里使用了$l_1$范数损失函数,$G$使用的损失函数与$S$的一致,但是要增大梯度(即增大$V$和$S$之间的差距)
关于目标模型$V$的梯度计算:
$V$是个黑盒,所以采用梯度逼近的方法来计算其梯度。但是$S$的训练不依赖$V$的参数$θ_V$,但是$G$的训练需要。
具体的算法如下所示。在每个epoch中,$G$和$S$分别训练$n_G$和$n_S$次,$n_G$和$n_S$的大小关系是个tradeoff

3.2 Loss Function
选择的损失函数都是知识蒸馏问题中常用的
【注】$K$是类的数量
KL散度(相对熵):
常用于数据蒸馏
即用概率分布 𝑞 来近似 𝑝 时所造成的信息损失量
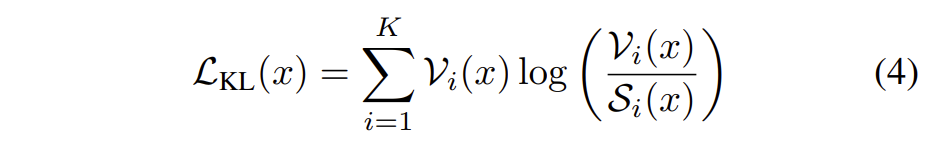
但是当$S$越来越接近$V$时,KL散度就有梯度消失的问题了,导致训练$G$时,难以收敛
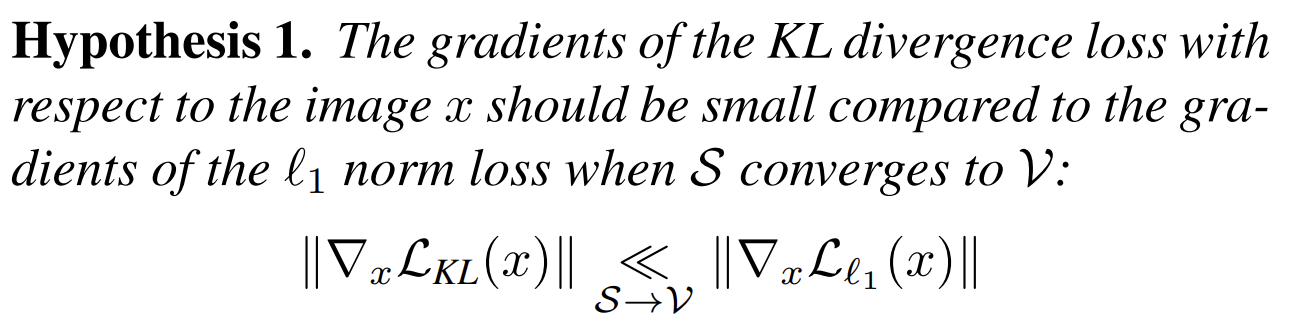
==$l_1$范数损失函数==(比KL散度简单),其中$v_i$和$s_i$都是softmax激活前的logits(即$w^Tx$)。但是$V$的参数不可知,所以需要logits(证明见附录)
【问题】这里计算$l_1$范数损失需要用到$V$的梯度吗
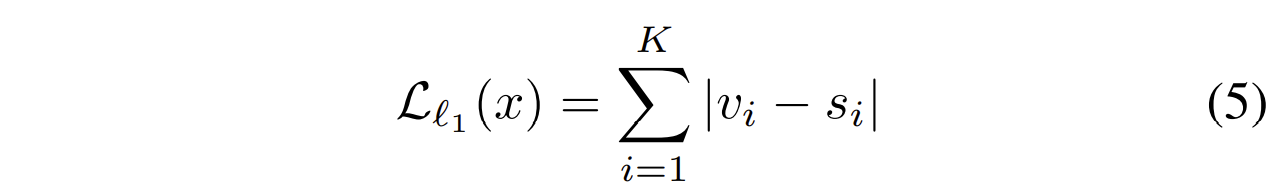
【问题】 3.3 Gradient Approximation(梯度逼近)
用零阶优化的方法。优化$G$时,通过逼近图像$x$的梯度,再使用反向传播算法来优化$G$,这样逼近的梯度的维度就很小????没明白

并使用前向差分法(forward differences method)来逼近梯度(即微分),==而不是选用零阶优化==
其中$u_i$是随机的方向向量,共$m$个
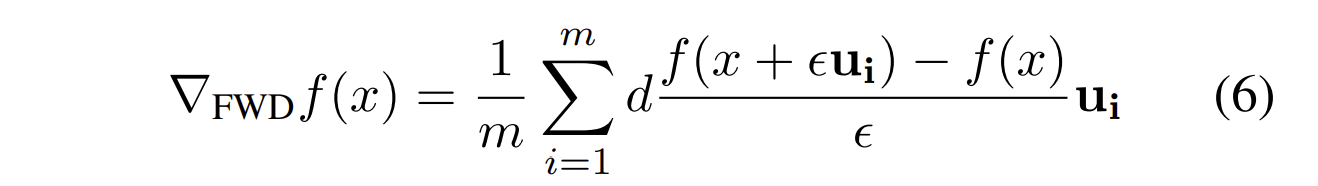
有限差分法也可以选用
【问题】零阶优化是一定要用到前向差分法吗,还是说梯度逼近需要用到前向差分
3.4 从概率分布中还原logits
首先,计算
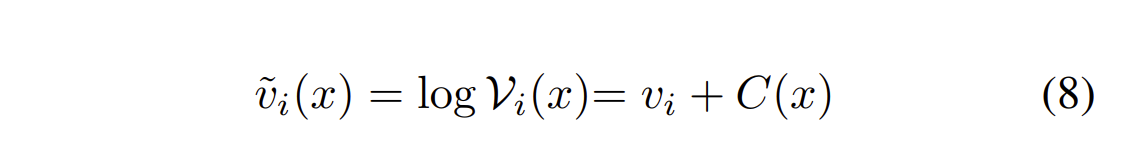
接着计算
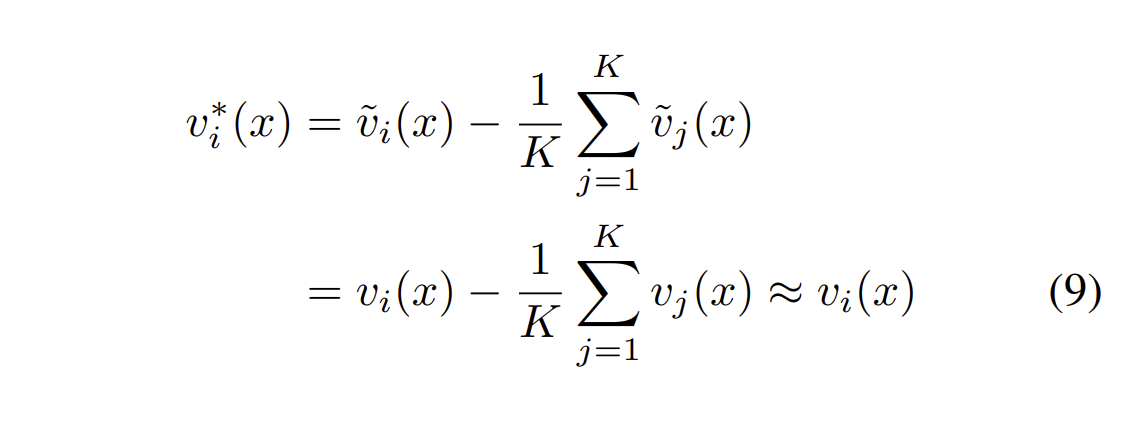
4 Experimental Validation
5 Ablation Studies
损失函数的选择
$l_1$范数损失函数要比KL散度损失函数好。KL散度损失函数收敛速度慢,而且会提前停止,存在梯度消失的问题
梯度逼近
在逼近梯度的过程中,方向向量$u_i$的问询次数$m$和梯度的准确度之间成正比关系,但是$m$越大,训练时候的开销就越大,所以这也是个tradeoff问题。在训练过程中,训练$S$使用的问询次数的占比为$\frac{n_S}{n_S+(m+1)n_G}$
作者提出了一种混合模式:先从一个surrogate dataset中提取出一个可能较差的student model,然后再用DFME中的算法,通过对目标模型的问询,来优化提取出的student model
logits的准确率的影响
当logits的均方差MAE比较小的时候,就可以从分布中还原出来
【论文笔记】Data-Free Model Extraction(CVPR 2021)
